만유인력의 법칙 - 개념, 공식 및 표현
우리는 만유인력의 법칙이 무엇인지, 그 공식과 진술이 무엇인지 설명합니다. 또한 공식 사용의 예입니다.

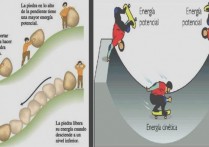
만유인력의 법칙은 물체의 중력 상호작용을 설명합니다.
만유인력의 법칙이란 무엇입니까?
만유인력의 법칙은 아이작 뉴턴이 1687년 저서 자연 철학의 원리 수학(Philosophiae Naturalis Principia Mathematica) 에서 공식화한 물리 법칙 중 하나입니다. 이는 거대한 물체 사이의 중력 상호 작용을 설명하고 중력 과 물체의 질량 의 비례 관계를 설정합니다. .
이 법칙을 공식화하기 위해 뉴턴은 두 질량이 서로 끌어당기는 힘은 두 질량을 두 질량을 분리하는 거리의 제곱으로 나눈 값에 비례한다고 추론했습니다. 이러한 추론은 관찰을 통한 실증적 검증의 결과이다 .
이 법칙은 두 물체가 더 가깝고 무거울수록 서로를 더 강하게 끌어당긴다는 것을 의미합니다 . 다른 뉴턴의 법칙과 마찬가지로 이는 당시 과학 지식 의 도약을 의미했습니다 .
그러나 오늘날 우리는 특정 질량을 초과하면 이 법칙이 타당성을 잃으며 (초거대 물체의 경우) 알베르트 아인슈타인이 1915년에 공식화한 일반 상대성 법칙을 적용해야 한다는 것을 알고 있습니다. 우주 중력의 법칙은 아인슈타인의 법칙에 근접한 것이지만 태양계 의 대부분의 중력 현상을 이해하는 데 여전히 유용합니다 .
도움이 될 수 있습니다: 과학적 방법
만유 인력의 법칙에 대한 진술
이 뉴턴 법칙의 공식 진술은 다음과 같이 유지됩니다.
“ 두 물체가 서로 끌어당기는 힘은 질량의 곱에 비례하고, 두 물체 사이의 거리의 제곱에 반비례합니다 .”
이는 두 물체가 질량이 더 크거나 작은지, 그리고 두 물체 사이의 거리에 따라 더 크거나 작은 힘으로 서로 끌어당긴다는 것을 의미합니다.
만유인력 법칙의 공식
만유 인력의 법칙의 기본 공식은 다음과 같습니다.
F = | (G . m 1 . m 2 ) / r² | . 아르 자형*
어디:
F는 두 질량 사이 의 인력 입니다 .
G는 만유 중력 상수 (6.673484.10 -11 Nm 2 /kg 2 ) 입니다 .
m 1 은 몸체 중 하나의 질량 입니다 .
m 2는 다른 물체의 질량 입니다 .
r 그들을 분리하는 거리 .
r*은 힘의 방향을 나타내는 단위 벡터입니다.
각 몸체의 인력을 계산하면(질량 1이 질량 2에 가하는 힘 또는 그 반대의 힘) 모듈에서는 동일하고 방향은 반대인 두 개의 힘이 있을 것입니다. 이러한 부호 차이를 얻으려면 방정식을 다음과 같이 작성해야 합니다.
F12 = | G. m 1 .m 2 / (r1 1 -r 2 ) 3 | . (r 1 -r 2 )
1을 2로 변경하면 각 경우에 대한 힘을 얻을 수 있습니다. 이런 방식으로 작성된 벡터 (r 1 -r 2 ) 는 각 힘에 대한 올바른 방향 ( 부호)을 제공합니다.
만유 인력의 법칙의 예
이 공식을 적용한 예로서 몇 가지 연습 문제를 풀어보겠습니다.
800kg의 질량과 500kg의 질량이 3m 떨어진 진공 속에서 서로 끌어당긴다고 가정해 보겠습니다. 그들이 경험하는 끌어당김의 힘을 어떻게 계산할 수 있나요 ?
간단히 공식을 적용하면 다음과 같습니다.
F = G.(m 1 .m 2 )/r 2
F = (6.67×10 -11 Nm 2 /kg 2 ) 입니다 . (800kg . 500kg) / (3m) 2
그리고 F = 2.964 x 10 -6 N 입니다.
또 다른 연습 문제: 질량이 1kg인 두 물체를 1N의 힘으로 서로 끌어당기려면 어느 거리에 놓아야 할까요?
같은 공식에서 출발
F = G.(m 1 .m 2 )/r 2
우리는 r 2 = G.(m 1 .m 2 )/ F 를 남겨두고 거리를 구할 것입니다.
또는 동일한 것은 무엇입니까: r = √ (G.[m 1 .m 2 ])/ F
즉, r = √ (6.67×10 -11 Nm 2 /kg 2 . 1kg x 1kg) / 1N
결과는 r = 8.16 x 10 -6 미터입니다.
계속하기: 중력장